Part 3: The Pair Selection Puzzle

How to ask the right questions when you can't ask them all

---

The Story So Far

In Part 1, we established the problem: ranking 237 pendants using pairwise comparisons. In Part 2, we learned how TrueSkill models each pendant with a belief distribution—$\mu$ for estimated appeal, $\sigma$ for uncertainty.

Now comes the crucial question: which pairs should we compare?

---

The Exploration-Exploitation Dilemma

After 20 comparisons, the app knows a few things:

• Pendant #47 (the rose gold teardrop) has won 6 of 7 matches. It's looking good.
• Pendant #183 has never been compared. Complete mystery.
• Pendant #12 has been compared 5 times with mixed results. Medium confidence.

Now, which pair should I see next?

Option A: Exploit what we know Compare #47 against its closest rivals. Refine the top of the ranking. Make sure our current best is actually the best.

Option B: Explore the unknown Compare #183 (never seen!) against something. Maybe it's the hidden gem that beats everything?

This is the classic exploration-exploitation tradeoff—one of the most studied problems in machine learning and decision theory.[^1]

Figure 1: The fundamental tradeoff. Pure exploitation might miss better options; pure exploration wastes comparisons on known mediocre items. We need a principled balance.

Lean too hard into exploitation, and you might miss a better option hiding in the unexplored items.

Lean too hard into exploration, and you waste comparisons on items you already know are mediocre.

We need a principled way to balance.

---

The Naive Approaches (And Why They Fail)

Random Selection: Pick any two items at random.

• ❌ Wastes comparisons on items we already know well
• ❌ Shows obviously mismatched pairs (uninformative)
• ❌ Can repeat the same pair annoyingly often

Round-Robin: Always compare the two items with fewest comparisons.

• ✅ Ensures every item gets exposure
• ❌ Doesn't account for match quality (#1 vs #200 teaches nothing)
• ❌ Ignores uncertainty—some items need more matches than others
• ❌ Diminishing returns: after 10 matches, another helps less

Close Match Heuristic: Compare items with similar $\mu$ values.

• ✅ Close matches are more informative
• ❌ Ignores uncertainty ($\sigma$)
• ❌ Gets stuck showing the same competitive pairs repeatedly
• ❌ Never explores new, uncertain items

We need something smarter.

---

E[Δσ]: Expected Uncertainty Reduction

Here's the key insight from Bayesian active learning: we should pick the pair that will teach us the most.

But "teach us the most" is vague. How do we quantify it?

Answer: measure how much uncertainty will shrink.

For any pair (i, j), we can compute the Expected Δσ (EΔσ)—the expected reduction in total uncertainty after comparing them.

$$E[\Delta\sigma]_{i,j} = \sum_{y \in \{L, R, D\}} P(y) \cdot \Delta\sigma_y$$

Where:

• $y$ ranges over possible outcomes: Left wins (L), Right wins (R), Draw (D)
• $P(y)$ is the probability of that outcome
• $\Delta\sigma_y$ is the uncertainty reduction if that outcome occurs

Computing Outcome Probabilities

TrueSkill gives us a generative model: preferences produce noisy choices, and the higher preference wins.

For two pendants with ratings $(\mu_L, \sigma_L)$ and $(\mu_R, \sigma_R)$:

1. Compute outcome probabilities: Use TrueSkill's generative model to predict $P(\text{Left wins})$, $P(\text{Right wins})$, and $P(\text{Draw})$ based on the $\mu$ gap and combined uncertainty.

2. Simulate hypothetical updates: For each outcome, compute what the new $\sigma$ values would be after running TrueSkill's update.

3. Calculate expected reduction:

   $$E[\Delta\sigma] = \sum_{y} P(y) \cdot (\sigma_\text{before} - \sigma_\text{after}(y))$$

(See expected_sigma_reduction() in backend/pair_selection.py for implementation details)

Why EΔσ Works

This formula naturally captures everything we care about:

Situation	E[Δσ] Result	Why
Both items uncertain (high $\sigma$)	High	Lots of uncertainty to reduce
One item uncertain	Medium	Still something to learn
Both items well-known (low $\sigma$)	Low	Not much uncertainty left
Close match (similar $\mu$)	Higher	Uncertain outcome = balanced learning
Lopsided match	Lower	One outcome dominates, less total info

The beauty is that we don't need any heuristic bonuses or special cases. The math just does the right thing.

---

Thompson Sampling: Randomness as a Feature

E[Δσ] is powerful, but it has a flaw: it's deterministic.

Given the same state, it always picks the same pair. This can lead to:

• Getting stuck in loops
• Over-focusing on a small set of "most informative" pairs
• Missing items that would be informative with a little more exploration

Enter Thompson Sampling, a beautifully simple algorithm from 1933 (!).

The Algorithm

1. For each pendant, sample an appeal value from its posterior: $\text{sample} \sim \mathcal{N}(\mu, \sigma^2)$
2. Sort all pendants by their sampled appeal
3. Consider adjacent pairs in this sampled ranking
4. Score them with E[Δσ] and pick the best

(See thompson_sample_pairs() in backend/pair_selection.py)

Why Thompson Works

The magic is in the sampling:

• High-$\sigma$ items have wide distributions → their samples fluctuate wildly

• Sometimes they sample high (appear at top of ranking)

• Sometimes they sample low (appear at bottom)

• This means they naturally end up in comparisons more often!

• Low-$\sigma$ items have narrow distributions → samples are consistent

• They stay near their true position

• Only appear in comparisons when they're actually competitive

Thompson Sampling is a natural explore-exploit balance: uncertain items get explored, certain items only compete when relevant.

---

The Hybrid Approach

Pure EΔσ is too greedy. Pure Thompson is too random.

Solution: combine them.

# Pseudo-code for hybrid selection
if random() < 0.25:
    candidates = thompson_sample_pairs()  # Sample from posteriors
else:
    candidates = all_pairs()              # Consider all O(n²) pairs

best = max(candidates, key=expected_sigma_reduction)
return best

(See choose_next_pair() in backend/pair_selection.py)

The hybrid approach:

• 75% of the time: Pure EΔσ on all pairs (greedy, efficient)
• 25% of the time: Thompson Sampling to generate candidates, then EΔσ to pick the best

This gives us:

• Efficiency from greedy EΔσ selection
• Exploration from Thompson's posterior sampling
• No loops (Thompson adds randomness)
• Principled (everything is Bayesian)

---

Handling Skips and Draws

One final detail: cooldown periods.

If you skip a pair or declare a draw, the algorithm excludes that pair from the next 2 comparisons. This prevents annoying repeats while still allowing highly informative pairs to resurface later if needed.

(Implemented via _get_recent_skips_and_draws() which queries the last N match records)

---

The Complete Algorithm

Putting it all together:

---

Results: Does It Work?

After implementing this hybrid algorithm, I tested it on my 237 pendants.

Before (random selection):

• 100+ comparisons before rankings stabilized
• Kept showing obviously mismatched pairs
• Top 3 kept changing even after 80 comparisons

After (hybrid E[Δσ] + Thompson):

• ~50 comparisons to stable top 10
• Pairs felt "meaningful"—close matches that were hard to decide
• Top 3 locked in by comparison #45

The difference is dramatic. Instead of wasting comparisons on obvious mismatches, every pair feels like it matters.

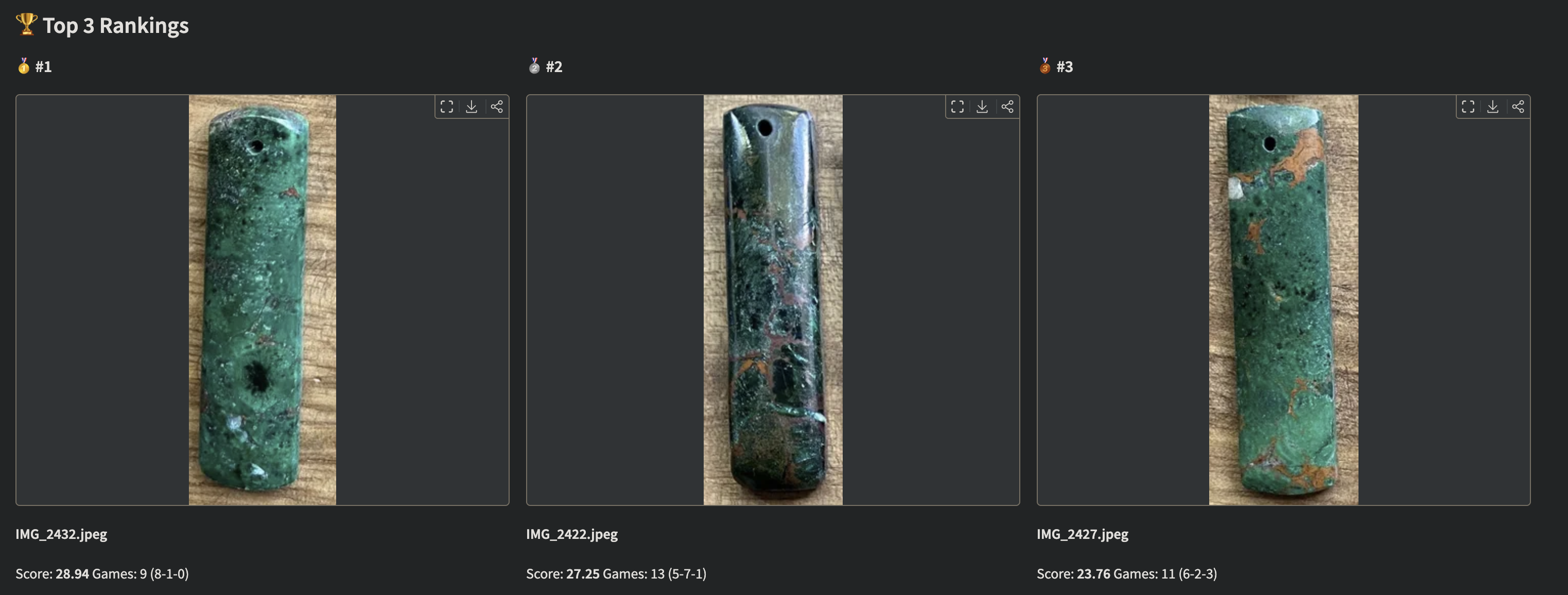Figure 2: The final leaderboard, ranked by conservative score ($\mu - 3\sigma$). The top 3 are clearly separated from the rest, with high confidence (low $\sigma$) after just 47 comparisons.

---

The Implementation

The complete algorithm combines:

1. Policy selection: 75% greedy E[Δσ], 25% Thompson sampling
2. Candidate generation: Either all O(n²) pairs or Thompson's adjacent pairs
3. Scoring: E[Δσ] for each candidate, with penalties for recent repeats
4. Filtering: Exclude recently skipped/drawn pairs (cooldown)
5. Selection: Return the highest-scoring valid pair

(See choose_next_pair() in backend/pair_selection.py for full implementation)

---

Key Takeaways

1. E[Δσ] is the gold standard for active learning in pairwise ranking. It directly measures expected information gain.

2. Thompson Sampling adds healthy randomness by sampling from posteriors, naturally balancing exploration and exploitation.

3. The hybrid approach (75% E[Δσ], 25% Thompson) combines their strengths while avoiding their weaknesses.

4. TrueSkill does the heavy lifting. The quality_1vs1() and rate_1vs1() functions give us everything we need for probabilistic reasoning about preferences.

5. Cooldowns prevent annoyance. Nobody wants to see the same pair twice in a row after skipping.

---

Epilogue: The Pendant

After 47 comparisons, the app converged. My top 3 were:

1. 🥇 Rose gold teardrop with subtle diamond accent
2. 🥈 Minimalist gold circle (surprisingly close!)
3. 🥉 Vintage-inspired cameo with modern twist

I went with #1. Valentine's Day was saved.

And along the way, I learned more about Bayesian statistics and preference learning than any textbook could have taught me.

Sometimes the best way to learn is to have a problem you actually care about solving.

---

The full source code is available at github.com/hugocool/product_picker

Previous: Part 2 - TrueSkill Demystified

Start from the beginning: Part 1 - The Pendant Problem